

A football kicked off by a player a ball thrown by a cricketer and a missile fired from a launching pad, all projected at some angles with the horizontal, are called projectiles. It is not necessary that an object should be thrown with some initial velocity in the horizontal direction. Since initial velocity is zero, hence, vertical distance y by using the second equation of motion is given by: This vertical motion is the same as for a freely falling body. It will accelerate downward under the force of gravity and hence a = g. But this time is given and is equal to 3 seconds.The vertical motion of the ball is also not complicated. The maximum height occurs at t = -Vo / 2(-16).The height H of a projectile thrown upward from ground (initial height = 0 or Ho = 0) is given by.Three seconds later, it reaches a maximum height. Solve the above for Ho to find the height of the buildingįrom ground, an object is thrown upward with an initial speed Vo.Ho is the initial height or height of the building. The initial speed Vo is known and also when t = 5 seconds H = 0 (touches the ground). The formula for the height H of a projectile thrown upward is given by.We now calculate the height H of the wellįrom the top of a building, an object is thrown upward with an initial speed of 64 ft/sec.The above equations has two solutions and only one of them is positive and is given by.The above is a quadratic equation that may be written as.We now substitute T2 by 3 - T1 in the above equation.Eliminate H and combine the equations H = 16 T1 2 and H = 1100 T2 to obtain.
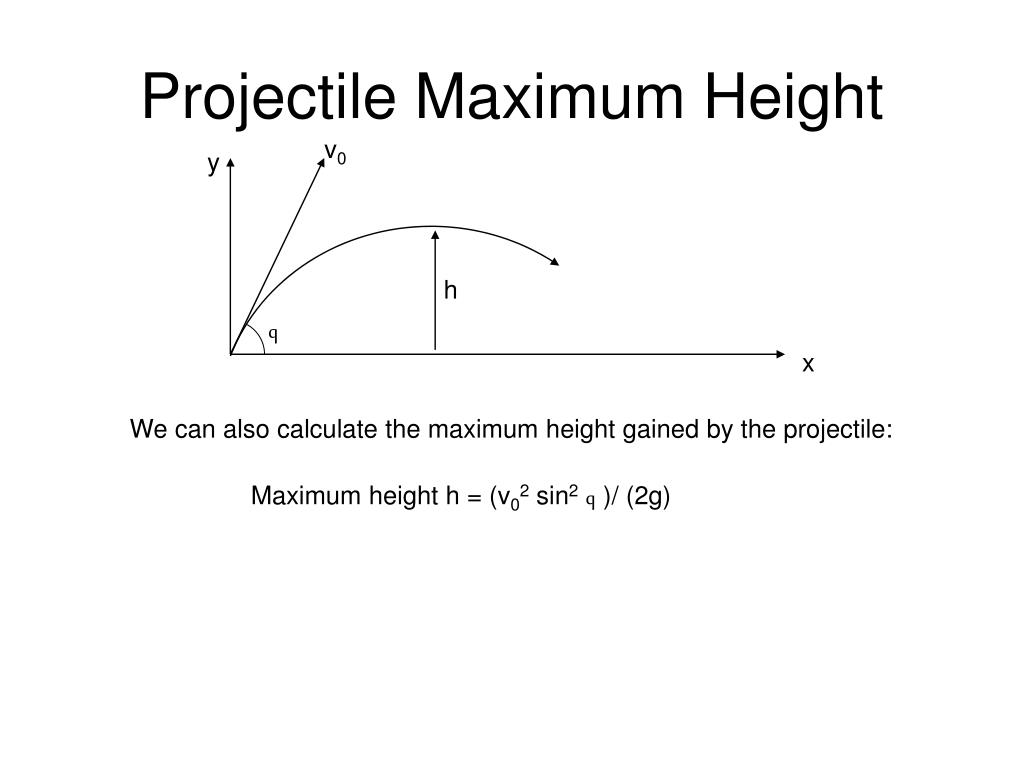

Let T2 be the time it takes sound wave to reach the top of the well.If H is the height of the well, we can write Let T1 be the time it takes the rock to reach the bottom of the well.If the water splash is heard 3 seconds after the rock was dropped, and that the speed of sound is 1100 ft / sec, approximate the height of the well. The graph below is that of h in terms of t and clearly shows that h is greater than 90 feet for t between 0.4 and 1.6 seconds.Ī rock is dropped into a well and the distance traveled is 16 t 2 feet, where t is the time.The height of the object is higher than 90 feet for.d - The object is higher than 90 feet for all values of t statisfying the inequality h > 90.The graphical meanings to the answers to parts a, b and c are shown below. So it takes 3.5 seconds fopr the object to hit the ground after it has been thrown upward. The above quadratic equation has two solutions one is negative and the second one is positive and approximately equal to 3.5 seconds.c - At the ground h = 0, hence the solution of the equation h = 0 gives the time t at which the object hits the ground.b - It takes 1 second for the object to reach it highest point.1 second after the object was thrown, it reaches its highest point (maximum value of h) which is given by.Hence for h given above the vertex is at t For a quadratic function of the form h = a t 2 + b t + c, the vertex is located at t = - b / 2a. The graph of h as a function of time t gives a parabolic shape and the maximum height h occur at the vertex of the parabola. a - The height h given above is a quadratic function.The formula h (t) = -16 t 2 + 32 t + 80 gives the height h above ground, in feet, of an object thrown, at t = 0, straight upward from the top of an 80 feet building.Ī - What is the highest point reached by the object?ī - How long does it take the object to reach its highest point?Ĭ - After how many seconds does the object hit the ground?ĭ - For how many seconds is the hight of the object higher than 90 feet? Projectile Problems with Detailed Solutions If an object is dropped, the distance traveled by this object is given byĪnd with a negative, the maximum of H occur at t = - b / 2a (vertex of the graph of H). Where g is the acceleration due to gravity which on earth is approximately equal to 32 feet / s 2, Vo is the initial velocity (when t = 0 ) and Ho is the initial height (when t = 0). If air resistance is ignored, the height h of a projectile above the ground after t seconds is given by Detailed solutions to the problems are provided. A tutorial on solving projectile problems.


 0 kommentar(er)
0 kommentar(er)
